Analisis Impedansi, Impedansi Masukan, dan Impedansi Keluaran

Impedansi adalah istilah kolektif untuk resistansi dan reaktansi, dan perbedaan terbesar antara resistansi dan reaktansi adalah bahwa pembatas arus resistansi (hukum Ohm) mengkonsumsi energi listrik pada saat yang bersamaan. Reaktansi terbatas pada arus dan tidak memakan energi listrik (tanpa melakukan usaha). Resistansi memiliki efek arus yang terbatas pada arus searah dan arus bolak-balik, sedangkan reaktansi hanya memiliki efek arus yang terbatas pada lingkungan arus bolak-balik.

Impedansi masukan mengacu pada impedansi ekivalen pada ujung masukan suatu rangkaian. Tambahkan sumber tegangan U pada terminal masukan dan ukur arus I pada terminal masukan, maka impedansi masukan Rin adalah U/I. Anda dapat membayangkan ujung masukan sebagai dua ujung resistor, dan nilai resistansi resistor ini adalah impedansi masukan.

Impedansi masukan tidak berbeda dengan komponen reaktansi biasa, karena mencerminkan besarnya efek pemblokiran arus.

Untuk rangkaian yang digerakkan tegangan, semakin besar impedansi masukan, semakin ringan beban pada sumber tegangan, sehingga lebih mudah untuk digerakkan tanpa mempengaruhi sumber sinyal; Untuk rangkaian yang digerakkan arus, semakin kecil impedansi masukan, semakin ringan beban pada sumber arus.

Impedansi Output

Impedansi keluaran mencakup impedansi internal dari sumber tegangan setara (rangkaian setara Thevenin) atau sumber arus setara (rangkaian setara Norton) dari port keluaran jaringan daya independen. Nilainya sama dengan impedansi masukan yang dilihat dari port keluaran ketika catu daya independen disetel ke nol.

Terlepas dari sumber sinyal, amplifier, dan catu daya, ada masalah dengan impedansi keluaran. Impedansi keluaran adalah resistansi internal sumber sinyal. Awalnya, untuk sumber tegangan ideal (termasuk catu daya), resistansi internal harus 0, atau impedansi sumber arus ideal harus tak terbatas. Impedansi keluaran memerlukan perhatian paling khusus dalam desain rangkaian.

Pada kenyataannya, sumber tegangan tidak dapat mencapai hal ini, dan sumber tegangan ideal sering kali dihubungkan secara seri dengan resistor r untuk setara dengan sumber tegangan sebenarnya. Resistor r yang dirangkai seri dengan sumber tegangan ideal adalah resistansi internal sumber sinyal/output amplifier/catu daya.

Ketika sumber tegangan ini menyuplai daya ke beban, arus I akan mengalir melalui beban dan menghasilkan I pada resistor ini × Penurunan tegangan r. Hal ini akan mengakibatkan penurunan tegangan keluaran catu daya, sehingga membatasi daya keluaran maksimum.

Demikian pula, sumber arus ideal harus memiliki impedansi keluaran tak terhingga, tetapi rangkaian sebenarnya tidak mungkin dilakukan.

Impedansi keluaran mengacu pada impedansi ekivalen rangkaian ketika beban rangkaian dilihat dari port keluaran rangkaian dalam arah yang berlawanan. Faktanya, ini terutama mengacu pada impedansi yang diukur oleh sumber energi pada ujung keluaran, yang umumnya dikenal sebagai resistansi internal.

Analisis Pemikiran Impedansi Rangkaian Switching

Seperti terlihat pada gambar berikut, V1 terus mengalirkan arus ke R1, dan rangkaian arus pada gambar ditunjukkan dengan panah hijau. Metode apa yang kita miliki jika kita ingin mengontrol aliran arus ke R1?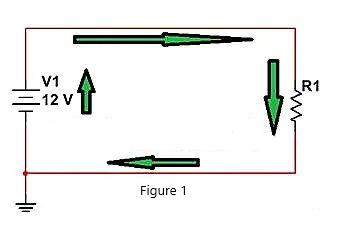

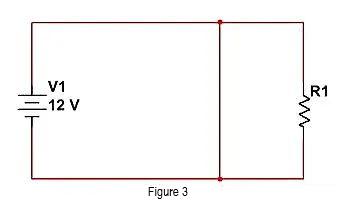
Cara yang paling umum adalah dengan memutus hubungan antara V1 dan R1 dan memutus rangkaian arus. Seperti yang ditunjukkan pada gambar berikut.

Alternatifnya, kita dapat melewati R1 seperti yang ditunjukkan pada gambar berikut. Tambahkan kawat di depan R1 untuk mengarahkan arus menuju jalur dengan impedansi rendah, dan R1 akan memperoleh arus yang dapat diabaikan.

Dua metode di atas sangat mudah, baik memutus sepenuhnya jalur dari V1 ke R1 atau membuat hubungan pendek R1, yang menyelesaikan masalah secara menyeluruh. Namun dalam dunia teknik, kita tidak bisa melakukannya dengan begitu bersih dan rapi, sering kali menekankan hal 'serupa'; mendekati. Jadi, pada "model hubung singkat", kita hanya dapat mencapai "impedansi rendah", sedangkan pada "model rangkaian terbuka", kita hanya dapat mencapai "impedansi tinggi". Jika energinya “dilemahkan” secara signifikan, kami yakin energi tersebut memenuhi standar.

Seperti yang ditunjukkan pada gambar di bawah, model beban daya sebenarnya ditampilkan. Mari kita lihat bagaimana mencapai efek peralihan dengan menyesuaikan impedansi. Dalam rangkaian sebenarnya, sumber daya memiliki batasan kapasitas keluaran dan hambatan internal, dan semakin besar arus keluaran, semakin rendah tegangan keluaran.

Rangkaian berikut mempunyai resistansi dalam 0,1 Ω dan beban 1K Ω. Dalam situasi saat ini, tegangan yang diperoleh pada kedua ujung beban terdiri dari resistansi internal dan tegangan parsial R2. Kita dapat menghitung V=5V * (1K/(1K+0.1))=4.9999V, I=5V/1000.1 Ω=4.9mA.

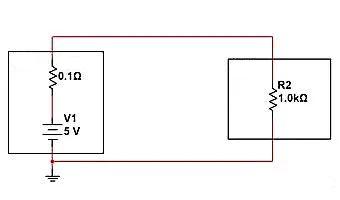
Jika kita menggunakan "model rangkaian terbuka" metode untuk memutus rangkaian, bagaimana kita mengatur impedansinya? Ini untuk menghubungkan resistor yang jauh lebih besar dari 1K secara seri antara catu daya dan beban, dan melakukan pembagian tegangan seri untuk mengurangi tegangan yang diperoleh pada R2. Seperti terlihat pada gambar berikut, jika sebuah resistor 1M dihubungkan secara seri dengan pembagi tegangan beban. Kita dapat menghitung distribusi tegangan akhir antara kedua ujung beban:

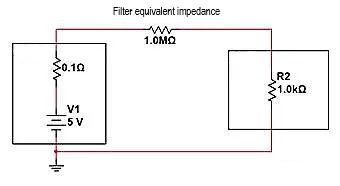
V=5V * (1K/(0,1+1000K+1K))=0,00499V, I=5V/1001000,1 Ω=0,0049mA. Amplitudonya telah melemah hampir 1000 kali lipat, dan dalam pemikiran teknik, R2 hampir "terputus".

Jika kita menggunakan "model hubung singkat" metode untuk memutuskan sambungan R2, bagaimana kita harus menyesuaikannya? Ini adalah untuk menghubungkan resistor yang jauh lebih kecil dari 0,1 Ω secara paralel di ujung depan beban dan melakukan pembagian tegangan seri dengan resistor internal, menghasilkan tegangan yang lebih kecil yang diperoleh pada R2.

Seperti yang ditunjukkan pada gambar berikut, jika ukuran penyaringan setara dengan resistor paralel 0,005 Ω dan pembagi tegangan resistansi internal. Kita dapat menghitung tegangan terdistribusi akhir antara kedua ujung beban R2:

V=5V * (0,0049/(0,1+0,0049)=0,233V. Amplitudo telah melemah hampir 20 kali lipat, dan dalam pemikiran teknik, R2 juga mirip dengan "terputus".

Di atas adalah model teoritis rangkaian saklar semikonduktor, dengan mengambil contoh rangkaian inverter:

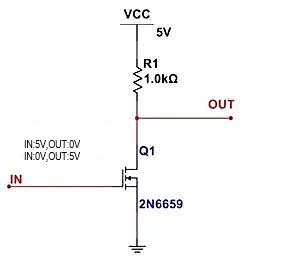
Ketika ujung IN dinyalakan, kita akan mengatakan bahwa transistor MOS Q1 sedang berjalan. Pada titik ini, keadaan konduksi setara dengan Q1 menjadi resistor dengan impedansi puluhan miliohm, dan kemudian membagi tegangan dengan resistor R1. Jika resistor pull-up R1 terlalu kecil dan juga puluhan miliohm, bahkan jika IN tinggi dan Q1 bekerja, terminal OUT tidak dapat mengeluarkan output pada level rendah.

Ketika ujung IN dimatikan, kita akan mengatakan bahwa transistor MOS Q1 terputus. Pada titik ini, keadaan cutoff setara dengan Q1 menjadi resistor dengan impedansi beberapa megaohm, dan membagi tegangan dengan resistor R1. Jika resistor pull-up R1 terlalu besar, yang juga beberapa megaohm, meskipun IN rendah dan Q1 terputus, terminal OUT tidak dapat menghasilkan output level tinggi.

Jadi ketika memahami rangkaian saklar secara mendalam, perlu untuk menganalisisnya dengan pemikiran impedansi.

Rangkaian Filter Analisis Pemikiran Impedansi

Di sini, analisis rangkaian penyaringan menggunakan pemikiran impedansi.

Dalam aplikasi teknik praktis, keluaran daya sering kali berisi komponen AC dengan frekuensi berbeda, baik yang kita inginkan maupun yang tidak kita inginkan. Impedansi induktansi dan kapasitansi akan bervariasi menurut frekuensi. Justru karena karakteristik inilah induktor dan kapasitor menjadi aktor utama dalam rangkaian penyaringan.

0-1GHz.

Seperti yang ditunjukkan pada gambar berikut, jika satu induktor 16uH dihubungkan secara seri antara catu daya dan beban, berapa besar peluruhan komponen AC 100MHz? Menurut rumus impedansi induktansi: ZL=2 π fL=2 * 3,14 * 100MHz * 16uH, ZL=10K dapat diperoleh.

Menurut rumus pembagi tegangan seri, tegangan/masukan di kedua ujung R3=R3/(R3+ZL)=1K/11K=0,0909. Jadi ketika amplitudo catu daya adalah 5V, amplitudo di kedua ujung R3 hanya 5V * 0,0909=0,45V.

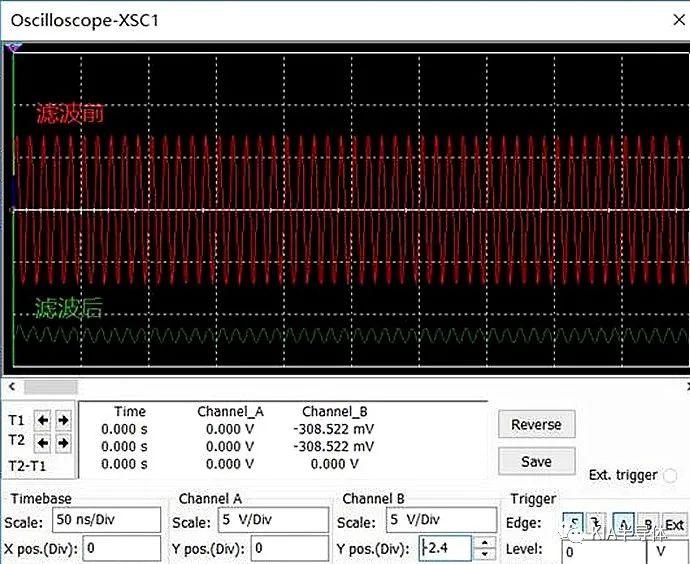
Pada 100MHz, gunakan osiloskop untuk mengukur bentuk gelombang sebelum dan sesudah pemfilteran. Perbandingan menunjukkan bahwa bentuk gelombang 100MHz berpengaruh, dan pengukuran sebenarnya adalah 0,449V, yang konsisten dengan hasil analisis.

Analisis pemikiran impedansi filter low-pass

Dengan menghubungkan induktor secara seri antara catu daya dan beban, dan menghubungkan kapasitor secara paralel di ujung depan beban, maka terbentuklah rangkaian filter lolos rendah.

Komponen AC 100MHZ?

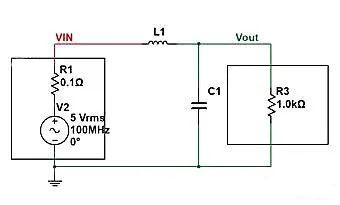
Pada titik ini, rangkaian dihubungkan secara paralel dengan impedansi Zc kapasitor (C1) dan R3, kemudian dibagi dengan impedansi ZL induktor (L1). Jadi kita dapat membuat daftar persamaan impedansi (yang merupakan rumus pembagi tegangan seri sederhana).

Amplitudo atenuasi=Vout/Vin=(Zc//R3)/(ZL+(Zc/R3)

Diantaranya, Zc=1/2 π fC dan ZL=2 π fL. Diketahui R3=1K Ω, dapat disimpulkan bahwa Zc=0.0015 Ω, Zc/R=0.00149 Ω.

ZL=13816 Ω, amplitudo redaman dapat diperoleh 0,00149/(13816,00149)=0,000000178.

Terlihat bahwa komponen AC 100MHz hampir tidak dapat melewati rangkaian low-pass filtering 22uH dan 1uF. Pada saat yang sama, kita juga melihat bahwa beban R3 dapat mempengaruhi efek penyaringan dari filter. Jadi terkadang kita menemukan bahwa rangkaian filter yang sama berfungsi dengan baik di sirkuit ini, tetapi buruk di sirkuit lain.